DCGAN 实现手写数字生成

题目

  1. 本次挑战使用的MNIST手写数字数据集，包含60,000张28x28的灰度图像，分为10个类别（数字0-9）。此数据集将用于训练你的生成对抗网络。
  2. 你的任务是使用DCGAN模型，对该数据集进行图像生成。具体要求如下：
    1. 数据集下载：请下载MNIST数据集，并确保数据集中包含训练集和测试集。
    2. 数据预处理：将图像数据进行必要的预处理，使其适合于DCGAN模型的训练。
    3. 模型训练：搭建DCGAN模型，并利用训练数据集进行训练，调整模型参数，尝试生成高质量的数字图像。
    4. 模型评估：在训练过程中，监控生成图像的质量，并可视化不同训练阶段生成的图像。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
import torchvision.utils as vutils
import os

batch_size = 128
lr = 0.0002
noise_dim = 100
epochs = 20
channel_size = 1

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
os.makedirs("output_dcgan", exist_ok=True)

# 数据预处理
transform = transforms.Compose([
    transforms.Grayscale(num_output_channels=1),
    transforms.ToTensor(),
    transforms.Normalize((0.5,), (0.5,))
])

# 使用 ImageFolder 读取数据
dataset = datasets.ImageFolder(root='data/mnist_jpg', transform=transform)
dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True)


class Generator(nn.Module):
    def __init__(self, noise_dim, channel_size):
        """
        基于卷积层的生成器
        实现生成器的若干卷积层的叠加
        :param noise_dim: 输入的噪音维度
        :param channel_size: 目标图像的通道数
        """
        super().__init__()
        self.main = nn.Sequential(
            nn.ConvTranspose2d(noise_dim, 64 * 2, kernel_size=7, stride=1, padding=0), # (batch_size, noise_dim, 1, 1) -> (batch_size, 128, 7, 7)
            nn.BatchNorm2d(64 * 2),
            nn.ReLU(True),

            nn.ConvTranspose2d(64 * 2, 64, kernel_size=4, stride=2, padding=1), # (batch_size, 128, 7, 7) -> (batch_size, 64, 14, 14)
            nn.BatchNorm2d(64),
            nn.ReLU(True),

            nn.ConvTranspose2d(64, channel_size, kernel_size=4, stride=2, padding=1), # (batch_size, 64, 14, 14) -> (batch_size, channel_size, 28, 28)
            nn.Tanh()
        )

    def forward(self, input):
        """完成前向传播"""
        return self.main(input)


class Discriminator(nn.Module):
    def __init__(self, channel_size):
        """
        基于卷积层的判别器
        实现判别器的若干卷积层的叠加
        :param channel_size: 欲判别的图像通道数
        """
        super().__init__()
        self.main = nn.Sequential(
            nn.Conv2d(channel_size, 64, kernel_size=4, stride=2, padding=1), # (batch_size, channel_size, 28, 28)->(batch_size, 64, 14, 14)
            nn.LeakyReLU(0.2, inplace=True),

            nn.Conv2d(64, 64 * 2, kernel_size=4, stride=2, padding=1), # (batch_size, 64, 14, 14)->(batch_size, 128, 7, 7)
            nn.BatchNorm2d(64 * 2),
            nn.LeakyReLU(0.2, inplace=True),
        )

        self.flatten = nn.Flatten()

        self.fc = nn.Sequential(
            nn.Linear(128 * 7 * 7, 1),
            nn.Sigmoid()
        )

    def forward(self, input):
        """
        完成前向传播
        :param input: 欲判别的图像数据
        :return: 返回分类结果
        """
        x = self.main(input)
        x = self.flatten(x)
        output = self.fc(x)
        return output

# 模型,优化器,损失函数
netG = Generator(noise_dim, channel_size).to(device)
netD = Discriminator(channel_size).to(device)

criterion = nn.BCELoss()

optimizerD = optim.Adam(netD.parameters(), lr=lr, betas=(0.5, 0.999))
optimizerG = optim.Adam(netG.parameters(), lr=lr, betas=(0.5, 0.999))

# 训练过程
for epoch in range(epochs):
    for i, (data, _) in enumerate(dataloader):
        # 训练判别器
            # 使 D_model 对真实数据集里的真实图像进行分类判断，将 label 视作 1
        netD.zero_grad()
        real_imgs = data.to(device)
        batch_size = real_imgs.size(0)

        label_real = torch.full((batch_size, 1), 1.0, device=device)
        output_real = netD(real_imgs)
        lossD_real = criterion(output_real, label_real)

            # 使 D_model 对 G_model 生成的虚假图像进行分类判断，将 label 视作 0
        noise = torch.randn(batch_size, noise_dim, 1, 1, device=device)
        fake_imgs = netG(noise)
        label_fake = torch.full((batch_size, 1), 0.0, device=device)
        output_fake = netD(fake_imgs.detach())
        lossD_fake = criterion(output_fake, label_fake)
            # 通过真实图像上的损失和虚假图像上的损失相加，得到原论文中的损失表达，可以衡量模型在真假图形分类上的表现
        lossD = lossD_real + lossD_fake
        lossD.backward()
        optimizerD.step()

        # 训练生成器
        netG.zero_grad()
        label_gen = torch.full((batch_size, 1), 1.0, device=device)   # 生成器希望判别器将假样本判为真实,故标签设置为 1
        output_gen = netD(fake_imgs)
        lossG = criterion(output_gen, label_gen)
        lossG.backward()
        optimizerG.step()

        if i % 100 == 0:
            print(f"Epoch [{epoch + 1}/{epochs}] Batch {i}/{len(dataloader)} Loss_D: {(lossD_real + lossD_fake).item():.4f} Loss_G: {lossG.item():.4f}")

    # 保存每个 epoch 的生成结果
    with torch.no_grad():
        fixed_noise = torch.randn(16, noise_dim, 1, 1, device=device)
        fake = netG(fixed_noise)
    vutils.save_image(fake, f"output_dcgan/fake_samples_epoch_{epoch + 1}.png", normalize=True)

结果

30 epoches:
alt text

project

GAN 实现手写数字生成

题目

  1. 本次挑战使用的MNIST手写数字数据集，包含60,000张28x28的灰度图像，分为10个类别（数字0-9）。此数据集将用于训练你的生成对抗网络。
  2. 你的任务是使用DCGAN模型，对该数据集进行图像生成。具体要求如下：
    1. 数据集下载：请下载MNIST数据集，并确保数据集中包含训练集和测试集。
    2. 数据预处理：将图像数据进行必要的预处理，使其适合于DCGAN模型的训练。
    3. 模型训练：搭建DCGAN模型，并利用训练数据集进行训练，调整模型参数，尝试生成高质量的数字图像。
    4. 模型评估：在训练过程中，监控生成图像的质量，并可视化不同训练阶段生成的图像。

代码（增强数据版）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader
import torchvision.utils as vutils
import os

# 设置参数
batch_size = 128
lr = 0.0002
noise_dim = 100
epochs = 20

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
os.makedirs("output_ganpro", exist_ok=True)

# 数据预处理
transform = transforms.Compose([
    transforms.Grayscale(num_output_channels=1),  # 修改处理的默认的图像通道数
    transforms.ToTensor(),
    transforms.Normalize((0.5,), (0.5,))  # 将图像归一化到 [-1, 1]
])

# 使用 ImageFolder 读取数据
dataset = datasets.ImageFolder(root='data/mnist_jpg', transform=transform)
dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True)


class Generator(nn.Module):
    def __init__(self, noise_dim):
        """
        生成器，将输入的噪声通过 MLP
        :param noise_dim: 输入的噪声维度
        """
        super().__init__()
        self.main = nn.Sequential(
            # MLP
            nn.Linear(noise_dim, 256),
            nn.BatchNorm1d(256),
            nn.LeakyReLU(0.2, True),

            nn.Linear(256, 512),
            nn.BatchNorm1d(512),
            nn.LeakyReLU(0.2, True),

            nn.Linear(512, 1024),
            nn.BatchNorm1d(1024),
            nn.LeakyReLU(0.2, True),

            nn.Linear(1024, 28 * 28),
            nn.Tanh()
        )

    def forward(self, input):
        """
        :param input: 输入的噪声数据
        :return: 通过 MLP 生成的图像
        """
        output = self.main(input)
        output = output.view(-1, 1, 28, 28)
        return output

class Discriminator(nn.Module):
    def __init__(self):
        """
        判别器，将输入的图像通过 MLP 进行二分类
        """
        super().__init__()
        self.main = nn.Sequential(
            # MLP
            nn.Linear(28 * 28, 1024),
            nn.LeakyReLU(0.2, inplace=True),

            nn.Linear(1024, 512),
            nn.LeakyReLU(0.2, inplace=True),

            nn.Linear(512, 256),
            nn.LeakyReLU(0.2, inplace=True),

            # 使用 Sigmoid 映射到 [0,1]
            nn.Linear(256, 1),
            nn.Sigmoid()
        )

    def forward(self, input):
        output = self.main(input.view(-1, 28 * 28))
        return output

# 模型,优化器,损失函数
netG = Generator(noise_dim).to(device)
netD = Discriminator().to(device)

criterion = nn.BCELoss()

optimizerD = optim.Adam(netD.parameters(), lr=lr, betas=(0.5, 0.999))
optimizerG = optim.Adam(netG.parameters(), lr=lr, betas=(0.5, 0.999))

# 训练过程
for epoch in range(epochs):
    for i, (data, _) in enumerate(dataloader):
        # 训练辨别器
            # 使 D_model 对真实数据集里的真实图像进行分类判断，将 label 视作 1
        netD.zero_grad()
        real_images = data.to(device)
        batch_size = real_images.size(0)

        label_real = torch.full((batch_size, 1), 1.0, device=device)  # 真实标签为 1
        output_real = netD(real_images)
        lossD_real = criterion(output_real, label_real)

            # 使 D_model 对 G_model 生成的虚假图像进行分类判断，将 label 视作 0
        noise = torch.randn(batch_size, noise_dim, device=device)
        fake_images = netG(noise)
        label_fake = torch.full((batch_size, 1), 0.0, device=device)  # 假图像标签为 0
        output_fake = netD(fake_images.detach())  # detach 防止梯度流向生成器
        lossD_fake = criterion(output_fake, label_fake)

        # 更新判别器参数
        lossD = lossD_real + lossD_fake
        lossD.backward()
        optimizerD.step()


        # 训练生成器
        netG.zero_grad()
        label_gen = torch.full((batch_size, 1), 1.0, device=device)
        output_gen = netD(fake_images)
        lossG = criterion(output_gen, label_gen)
        lossG.backward()
        optimizerG.step()

        # 输出训练信息
        if i % 100 == 0:
            print(f"Epoch [{epoch + 1}/{epochs}] Batch {i}/{len(dataloader)} "
                  f"Loss_D: {(lossD_real + lossD_fake).item():.4f} Loss_G: {lossG.item():.4f}")

    # 每个 epoch 结束后保存一批生成的图片
    with torch.no_grad():
        fixed_noise = torch.randn(16, noise_dim, device=device)
        fake = netG(fixed_noise).detach()
    vutils.save_image(fake, f"output_ganpro/fake_samples_epoch_{epoch + 1}.png", normalize=True)

结果

30 epoches:
alt text

project

BERT 实现 IMDb 情感分类

题目

  1. 在本次挑战中，你将使用IMDb电影评论数据集，该数据集包含50,000条影评，其中25,000条用于训练，25,000条用于测试。每条评论都被标记为正面或负面情感。
  2. 你的任务是使用BERT模型，对该数据集进行情感分类。具体要求如下：
    1. 数据集下载：请下载IMDb数据集，确保数据集中包含train和test两个文件夹，分别用于训练和测试。
    2. 数据预处理：对文本数据进行必要的预处理，包括分词、去除停用词、填充等，以便用于BERT模型的训练。
    3. 模型训练：利用BERT模型对训练数据集进行训练，调整模型参数，使其在测试集上取得尽可能高的分类准确度。
    4. 模型评估：在训练过程中，及时监控模型在测试集上的性能，并记录模型在测试集上的分类准确率，将结果可视化（如损失函数，预测准确率等）。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, Dataset
from torch.optim.lr_scheduler import OneCycleLR  # type: ignore
from transformers import BertTokenizer, BertForSequenceClassification
from torchtext.datasets import IMDB
import matplotlib.pyplot as plt

# 设备设置
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# 加载 BERT 分词器
tokenizer = BertTokenizer.from_pretrained("bert-base-uncased")


def text_pipeline(text):
    """
    :param text: 原始文本
    :return: 处理后的 token id 和 attention mask
    """
    return tokenizer(text, padding="max_length", truncation=True, max_length=100, return_tensors="pt")


def label_pipeline(label):
    """
    :param label: 电影评论标签（pos/neg）
    :return: 1 表示正面，0 表示负面
    """
    return 1 if label == "pos" else 0


class IMDBDataset(Dataset):
    """自定义 IMDB 数据集类"""
    def __init__(self, data_iter):
        """
        :param data_iter: IMDB 数据集迭代器
        """
        self.data = []
        for label, text in data_iter:
            encoding = text_pipeline(text)
            self.data.append((
                encoding["input_ids"].squeeze(0),
                encoding["attention_mask"].squeeze(0),
                label_pipeline(label)
            ))

    def __len__(self):
        """返回数据集大小"""
        return len(self.data)

    def __getitem__(self, idx):
        """获取数据集中的单个样本"""
        return self.data[idx]


# 加载 IMDB 数据集
train_iter, test_iter = IMDB(split="train"), IMDB(split="test")
train_data, test_data = IMDBDataset(train_iter), IMDBDataset(test_iter)


def collate_fn(batch):
    """
    处理批量数据
    :param batch: 输入数据
    :return: 处理后的 input_ids, attention_masks, labels
    """
    input_ids, attention_masks, labels = zip(*batch)
    return torch.stack(input_ids), torch.stack(attention_masks), torch.tensor(labels, dtype=torch.long)


# 创建数据加载器
train_loader = DataLoader(train_data, batch_size=64, shuffle=True, collate_fn=collate_fn)
test_loader = DataLoader(test_data, batch_size=64, shuffle=False, collate_fn=collate_fn)

# 加载预训练 BERT 模型
model = BertForSequenceClassification.from_pretrained("bert-base-uncased", num_labels=1).to(device)

# 只训练 BERT 的最后 4 层
for param in model.bert.encoder.layer[:-4].parameters():
    param.requires_grad = False

# 定义优化器、损失函数和学习率调度器
optimizer = optim.AdamW(model.parameters(), lr=5e-5, weight_decay=1e-2)
criterion = nn.BCEWithLogitsLoss().to(device)

EPOCHS = 3
scheduler = OneCycleLR(
    optimizer,
    max_lr=5e-5,
    total_steps=EPOCHS * len(train_loader),
    pct_start=0.3,
    anneal_strategy='cos',
    div_factor=10,
    final_div_factor=100
)

# 训练模型
def train(model, loader, optimizer, criterion, scheduler):
    model.train()
    epoch_loss = 0
    for input_ids, attention_masks, labels in loader:
        input_ids, attention_masks, labels = input_ids.to(device), attention_masks.to(device), labels.to(device)

        optimizer.zero_grad()
        outputs = model(input_ids, attention_mask=attention_masks)
        logits = outputs.logits.squeeze(1)

        loss = criterion(logits, labels.float())
        loss.backward()
        optimizer.step()
        scheduler.step()

        epoch_loss += loss.item()
    return epoch_loss / len(loader)

# 评估模型
def evaluate(model, loader, criterion):
    model.eval()
    epoch_loss, correct, total = 0, 0, 0
    with torch.no_grad():
        for input_ids, attention_masks, labels in loader:
            input_ids, attention_masks, labels = input_ids.to(device), attention_masks.to(device), labels.to(device)

            outputs = model(input_ids, attention_mask=attention_masks)
            logits = outputs.logits.squeeze(1)

            loss = criterion(logits, labels.float())
            epoch_loss += loss.item()

            preds = torch.sigmoid(logits) > 0.5
            correct += (preds == labels).sum().item()
            total += labels.size(0)
    return epoch_loss / len(loader), correct / total


# 训练过程
train_losses, test_losses, test_accs = [], [], []
for epoch in range(EPOCHS):
    train_loss = train(model, train_loader, optimizer, criterion, scheduler)
    test_loss, test_acc = evaluate(model, test_loader, criterion)
    train_losses.append(train_loss)
    test_losses.append(test_loss)
    test_accs.append(test_acc)
    print(f'Epoch: {epoch + 1:02}, Train Loss: {train_loss:.3f}, Test Loss: {test_loss:.3f}, Test Acc: {test_acc:.2%}')

# 保存模型
torch.save(model.state_dict(), "bert_imdb.pth")

# 绘制训练曲线
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(train_losses, label="Train Loss")
plt.plot(test_losses, label="Test Loss")
plt.legend()
plt.title("Loss Curve")
plt.subplot(1, 2, 2)
plt.plot(test_accs, label="Test Accuracy")
plt.legend()
plt.title("Accuracy Curve")
plt.tight_layout()
plt.show()

结果

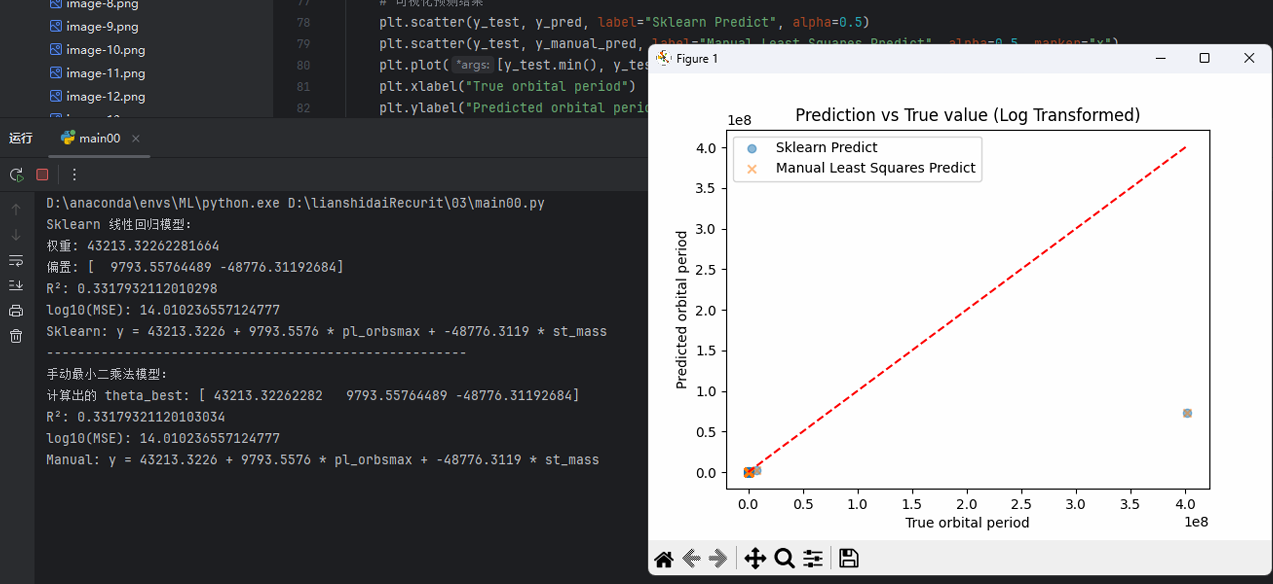
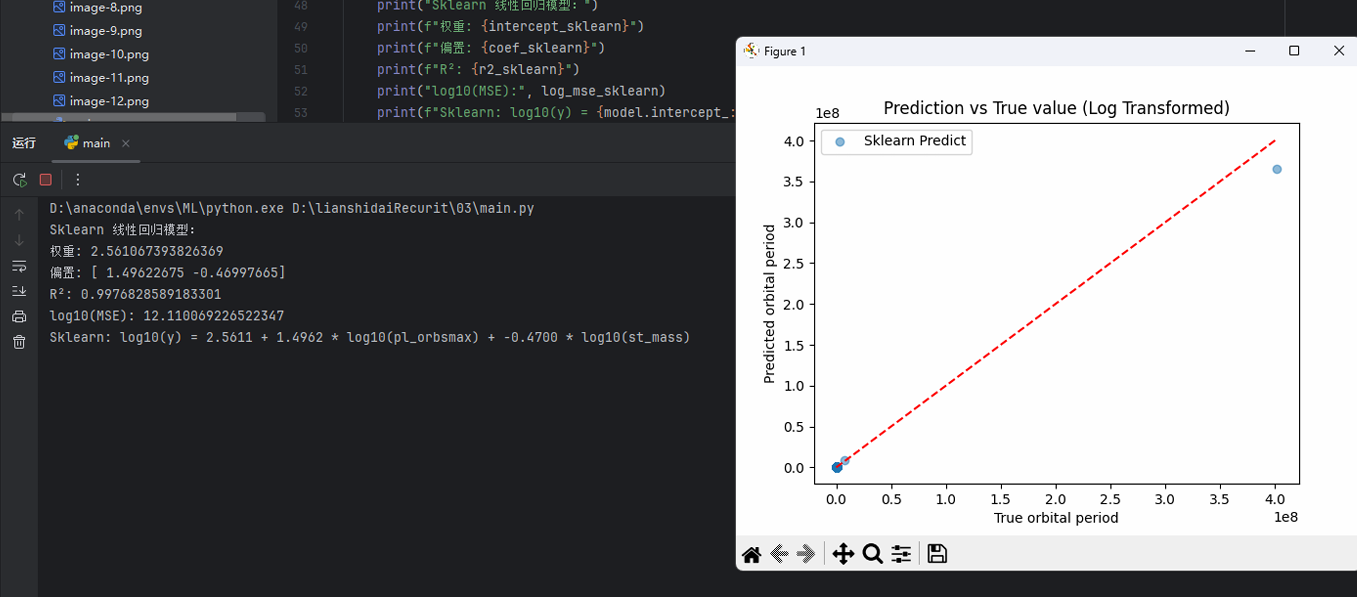
alt text

project

房价预测

题目

KaggleHouse Prices - Advanced Regression Techniques

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split, RandomizedSearchCV
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
import xgboost as xgb

# 读取数据
train_data = pd.read_csv('train.csv')
test_data = pd.read_csv('test.csv')

# 备份 test_data 的 ID 列
test_ids = test_data['Id']

# 处理缺失值
numeric_features = train_data.select_dtypes(include=[np.number]).columns.drop('SalePrice', errors='ignore')
non_numeric_features = train_data.select_dtypes(exclude=[np.number]).columns

# 数值型特征填充
train_data[numeric_features] = train_data[numeric_features].fillna(train_data[numeric_features].mean())
test_data[numeric_features] = test_data[numeric_features].fillna(test_data[numeric_features].mean())

# 类别型特征填充
for feature in non_numeric_features:
    train_data.loc[:, feature] = train_data[feature].fillna('Missing')
    test_data.loc[:, feature] = test_data[feature].fillna('Missing')

# 独热编码
train_data = pd.get_dummies(train_data)
test_data = pd.get_dummies(test_data)

# 确保特征对齐
train_data, test_data = train_data.align(test_data, join='left', axis=1, fill_value=0)

# 提取 X, y
X = train_data.drop('SalePrice', axis=1)
y = train_data['SalePrice']

# 划分训练集和验证集
X_train, X_valid, y_train, y_valid = train_test_split(X, y, test_size=0.2, random_state=42)

# 标准化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_valid_scaled = scaler.transform(X_valid)
X_test_scaled = scaler.transform(test_data.drop('SalePrice', axis=1, errors='ignore'))

# XGBoost 训练
xgb_model = xgb.XGBRegressor(objective='reg:squarederror', random_state=42, missing=np.nan)

# 超参数搜索
param_grid = {
    'learning_rate': [0.01, 0.1, 0.2],
    'max_depth': [3, 5, 7],
    'n_estimators': [100, 200, 300]
}
grid_search = RandomizedSearchCV(xgb_model, param_distributions=param_grid, n_iter=10, cv=3, scoring='neg_mean_squared_error', random_state=42)
grid_search.fit(X_train_scaled, y_train)

# 最优模型
best_model = grid_search.best_estimator_

# 预测
y_pred = best_model.predict(X_valid_scaled)
rmse = np.sqrt(mean_squared_error(y_valid, y_pred))
print(f"Validation RMSE: {rmse:.2f}")

# 测试集预测
test_predictions = best_model.predict(X_test_scaled)

# 生成提交文件
submission = pd.DataFrame({'Id': test_ids, 'SalePrice': test_predictions})
submission.to_csv('submission.csv', index=False)

mean_price = y_valid.mean()
relative_rmse = rmse / mean_price
print(f"Relative RMSE: {relative_rmse:.2%}")

project

Transformer 实现 IMDb 情感分类

题目

  1. 在本次挑战中，你将使用IMDb电影评论数据集，该数据集包含50,000条影评，其中25,000条用于训练，25,000条用于测试。每条评论都被标记为正面或负面情感。
  2. 你的任务是使用Transformer模型，对该数据集进行情感分类。具体要求如下：
    1. 数据集下载：请下载IMDb数据集，确保数据集中包含train和test两个文件夹，分别用于训练和测试。
    2. 数据预处理：对文本数据进行必要的预处理，包括分词、去除停用词、填充等，以便用于Transformer模型的训练。
    3. 模型训练：利用Transformer模型对训练数据集进行训练，调整模型参数，使其在测试集上取得尽可能高的分类准确度。
    4. 模型评估：在训练过程中，及时监控模型在测试集上的性能，并记录模型在测试集上的分类准确率，将结果可视化（如损失函数，预测准确率等）。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
import torch
import torch.nn as nn
import torch.optim as optim
from torch.optim.lr_scheduler import OneCycleLR  # type: ignore
from torchtext.datasets import IMDB
from torchtext.data.utils import get_tokenizer
from torchtext.vocab import build_vocab_from_iterator
from torch.utils.data import DataLoader, Dataset
import matplotlib.pyplot as plt
import numpy as np


# 定义文本分词器，使用 spaCy 进行英文分词
tokenizer = get_tokenizer("spacy", language="en_core_web_sm")

def collect_tokens(data_iter):
    """
    :param data_iter: IMDB数据集
    :return: 返回单词列表
    """
    all_tokens = []
    for _, text in data_iter:
        tokens = tokenizer(text)
        all_tokens.append(tokens)
    return all_tokens  # 返回所有 tokens 的列表

# 加载 IMDB 数据集
train_iter = IMDB(split="train")
test_iter = IMDB(split="test")

# 构建词汇表
vocab = build_vocab_from_iterator(collect_tokens(train_iter), max_tokens=20000, specials=["<pad>", "<unk>"])
vocab.set_default_index(vocab["<unk>"])  # 设置未记录的词用 <unk> 代替

def text_pipeline(text):
    """
    :param text: 欲处理的文本列表
    :return: 文本对应的索引列表
    """
    tokens = tokenizer(text)
    max_length = 100 # 只需要前 100 长度
    tokens = tokens[:max_length]
    index = []
    for token in tokens:
        index.append(vocab[token])
    return index

def label_pipeline(label):
    """
    :param label: 情感标签 pos 或 neg
    :return:  将 pos 或 neg 映射为 1 或 0
    """
    return 1 if label == "pos" else 0

class IMDBDataset(Dataset):
    """自定义 IMDB 数据集类，用于加载 IMDB 电影评论数据"""
    def __init__(self, data_iter):
        """
        初始化
        :param data_iter: 同时包含 （label，text） 的数据迭代器
        """
        self.data = []
        for label, text in data_iter:
            self.data.append((text_pipeline(text), label_pipeline(label)))

    def __len__(self):
        """
        :return: 返回数据集 self.data 长度
        """
        return len(self.data)

    def __getitem__(self, idx):
        """
        :param idx: 索引
        :return: 索引对应的单词
        """
        return self.data[idx]

# 创建训练集和测试集
train_data = IMDBDataset(train_iter)
test_data = IMDBDataset(test_iter)

def collate_fn(batch):
    """
    处理批量数据，对文本进行填充使其长度一致
    :param batch: 批量数据
    :return: 填充处理之后的结果
    """
    texts, labels = zip(*batch)

    lengths = []
    for text in texts:
        lengths.append(len(text))

    max_len = max(lengths)

    padded_texts = []
    for text in texts:
        padded_texts.append(text + [vocab["<pad>"]] * (max_len - len(text)))

    return torch.tensor(padded_texts), torch.tensor(labels, dtype=torch.float)

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

# 创建数据加载器
train_loader = DataLoader(train_data, batch_size=64, shuffle=True, collate_fn=collate_fn)
test_loader = DataLoader(test_data, batch_size=64, shuffle=False, collate_fn=collate_fn)

class PositionalEncoding(nn.Module):
    """ 定义位置编码类，为 Transformer 提供位置信息 """
    def __init__(self, d_model, dropout):
        """
        :param d_model: 词向量的维度
        :param dropout: Dropout 的概率，用于防止过拟合。
        """
        super().__init__()
        self.dropout = nn.Dropout(p=dropout)

        max_len = 5000 # 最大序列长度
        position_code = torch.zeros(max_len, d_model) # 储存位置编码

        position_item = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1) # 生成位置索引 形状是(max_len, 1)

        div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-np.log(10000.0) / d_model))  # 即 10000 ^ (-2i / d_model)

        position_code[:, 0::2] = torch.sin(position_item * div_term) # 偶数位置
        position_code[:, 1::2] = torch.cos(position_item * div_term) # 奇数位置

        self.register_buffer('position_code', position_code) # 将位置编码矩阵注册为模型不参与训练的缓冲区

    def forward(self, x):
        """
        前向传播
        :param x: 输入张量 (batch_size, seq_len, d_model)
        :return:  添加位置编码之后的张量
        """
        x = x + self.position_code[:x.size(1)] # 只取前 seq_len 个位置编码
        return self.dropout(x)

class TransformerClassifier(nn.Module):
    """ 定义 Transformer 分类模型 """
    def __init__(self, vocab_size, embed_dim, num_heads, num_layers, hidden_dim, dropout):
        """
        初始化
        :param vocab_size: 词汇表的大小
        :param embed_dim: 词嵌入的维度
        :param num_heads: Multi-Head 的头数
        :param num_layers: Encoder 的层数
        :param hidden_dim: FNN的隐藏层维度
        :param dropout: dropout 率
        """
        super().__init__()

        self.embedding = nn.Embedding(vocab_size, embed_dim) # 进行词嵌入，完成离散的索引->可学习的向量
        self.pos_encoder = PositionalEncoding(embed_dim, dropout) # 完成位置信息的添加

        encoder_layers = nn.TransformerEncoderLayer(d_model=embed_dim, nhead=num_heads, dim_feedforward=hidden_dim, dropout=dropout) # 编码器层，传入若干所需的参数

        self.transformer_encoder = nn.TransformerEncoder(encoder_layers, num_layers) # 完成若干个编码器层堆叠
        self.fc = nn.Linear(embed_dim, 1) # 全连接层，完成分类
        self.dropout = nn.Dropout(dropout) # Dropout 层

    def forward(self, text):
        """
        前向传播，完成计算流程
        :param text: 输入的文本张量 形状为 (batch_size, seq_len)
        :return:分类结果，形状为 (batch_size)
        """
        embedded = self.embedding(text) # 完成词嵌入映射，得到 (batch_size, seq_len, embed_dim)形状
        embedded = self.dropout(embedded) # dropout

        embedded = self.pos_encoder(embedded) # 添加位置编码

        embedded = embedded.transpose(0, 1) # 调整张量的维度为 (seq_len, batch_size, embed_dim)

        output = self.transformer_encoder(embedded) # 通过 Transformer 编码器
        output = output.mean(dim=0) # 对序列维度（seq_len）取均值，得到句子级别的表示， 形状变为 (batch_size, embed_dim)

        return self.fc(output).squeeze(1) # 通过全连接层，得到分类结果，形状为 (batch_size, 1)，然后去除多余的维度，返回的形状为 (batch_size)

# 设置模型参数
embed_dim = 512
num_heads = 4
num_layers = 4
hidden_dim = 512
dropout = 0.2
epochs = 10

# 初始化模型
model = TransformerClassifier(
    vocab_size=len(vocab),
    embed_dim=embed_dim,
    num_heads=num_heads,
    num_layers=num_layers,
    hidden_dim=hidden_dim,
    dropout=dropout
).to(device)


# 定义优化器和损失函数
optimizer = optim.AdamW(model.parameters(), lr=1e-4, weight_decay=1e-2)
scheduler = OneCycleLR(
    optimizer,
    max_lr=1e-4,         # 训练中最高学习率
    total_steps=epochs * len(train_loader),  # 总训练步数 = epoch数 * 每个epoch的batch数
    pct_start=0.3,       # warmup 30% 训练步数
    anneal_strategy='cos',  # 余弦退火策略
    div_factor=10,       # 初始学习率 = max_lr / 10
    final_div_factor=100 # 结束学习率 = max_lr / 100
)

criterion = nn.BCEWithLogitsLoss().to(device)

# 训练模型
def train(model, loader, optimizer, criterion, scheduler):
    model.train()
    epoch_loss = 0
    for text, label in loader:
        text, label = text.to(device), label.to(device)
        predictions = model(text)
        loss = criterion(predictions, label)
        optimizer.zero_grad()
        loss.backward()
        torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)
        optimizer.step()
        scheduler.step()

        epoch_loss += loss.item()
    return epoch_loss / len(loader)

# 评估模型
def evaluate(model, loader, criterion):
    model.eval()
    epoch_loss = 0
    correct, total = 0, 0
    with torch.no_grad():
        for text, label in loader:
            text, label = text.to(device), label.to(device)
            predictions = model(text)

            loss = criterion(predictions, label)
            epoch_loss += loss.item()
            preds = torch.sigmoid(predictions) > 0.5
            correct += (preds == label).sum().item()
            total += label.size(0)
    return epoch_loss / len(loader), correct / total

# 训练过程
train_losses, test_losses, test_accs = [], [], []

# 开始训练
for epoch in range(epochs):
    train_loss = train(model, train_loader, optimizer, criterion, scheduler)
    test_loss, test_acc = evaluate(model, test_loader, criterion)
    train_losses.append(train_loss)
    test_losses.append(test_loss)
    test_accs.append(test_acc)
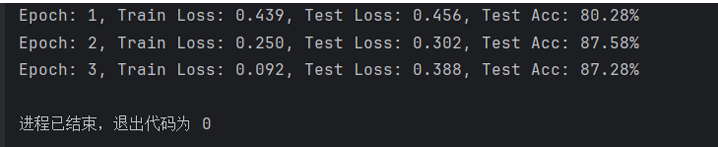
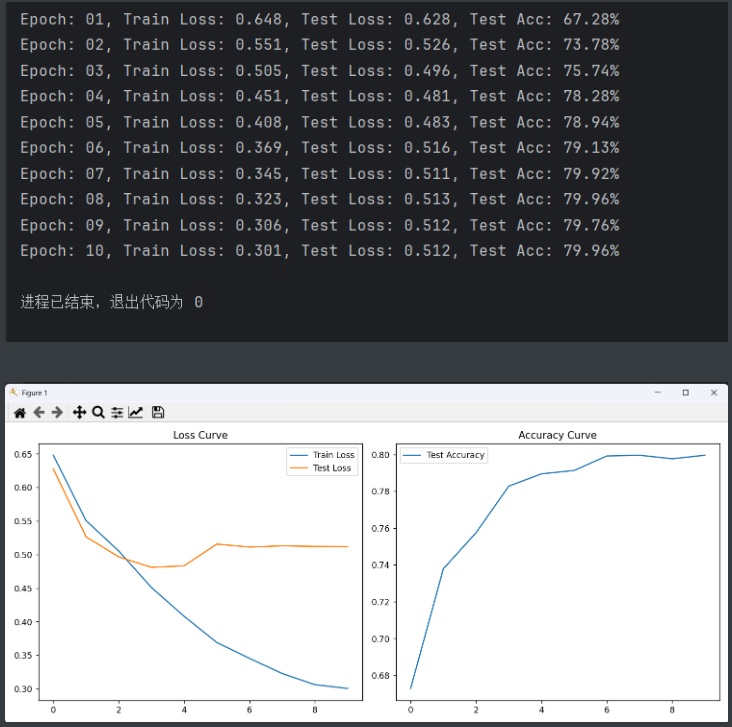
    print(f'Epoch: {epoch + 1:02}, Train Loss: {train_loss:.3f}, Test Loss: {test_loss:.3f}, Test Acc: {test_acc:.2%}')

# 保存训练后的参数信息
torch.save(model.state_dict(), "model.pth")
# 保存词汇表信息
torch.save(vocab, "vocab.pth")

# 绘制模型训练和评估的可视化图表
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(train_losses, label='Train Loss')
plt.plot(test_losses, label='Test Loss')
plt.legend()
plt.title('Loss Curve')
plt.subplot(1, 2, 2)
plt.plot(test_accs, label='Test Accuracy')
plt.legend()
plt.title('Accuracy Curve')
plt.tight_layout()
plt.show()

结果

alt text

project

预测系外行星轨道周期

任务

  • 使用 NASA系外行星数据库 中的数据
  • 选取轨道半长轴（pl_orbsmax）和母恒星质量（st_mass）作为输入特征
  • 目标变量为轨道周期（pl_orbper）

思路

导入必要的库

1
2
3
4
5
6
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

第一步： 访问 NASA 系外行星数据库，获取行星数据保存在 csv 文件中
第二步： 提取 csv 文件中所需要的数据，保留’pl_orbsmax’, ‘st_mass’和’pl_orbper’数据，与此同时注意到某些数据是缺失的，故而使用 df.dropna(subset=['pl_orbsmax', 'st_mass', 'pl_orbper']) 用来删除含有缺失值的数据组，保证后续计算正确

1
2
3
4
5
6
7
8
9
# 加载数据
df = pd.read_csv("D:/lianshidaiRecurit/03/PSCompPars_2025.02.09_07.27.02.csv")

# 处理缺失值
df = df.dropna(subset=['pl_orbsmax', 'st_mass', 'pl_orbper'])

# 选择相关特征和目标变量
X = df[['pl_orbsmax', 'st_mass']]
y = df['pl_orbper']

第三步： 使用提取到的数据来训练模型

首先需要将数据使用 train_test_split 来拆分成 8：2 的训练集和测试集，使用训练集来进行线性回归拟合

1
2
3
4
5
6
7
8
9
# 拆分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 使用 sklearn 进行线性回归
model = LinearRegression()
model.fit(X_train, y_train)

# 预测
y_pred = model.predict(X_test)

第四步： 使用 MSE、R检测法 来评估模型的预测性能

1
2
3
4
5
6
# 预测
y_pred = model.predict(X_test)

# 计算 sklearn 线性回归的 R^2 和 MSE
r2_sklearn = r2_score(y_test, y_pred)
mse_sklearn = mean_squared_error(y_test, y_pred)

第五步： 手动使用最小二乘法来完成线性回归的任务，这里具体的计算方法使用了 伪逆矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def manual(X_train, X_test, y_train, y_test):
    """手动实现最小二乘法计算参数"""
    # 偏置项
    X_b = np.c_[np.ones((len(X_train), 1)), X_train.values]
    # 伪逆法求解 theta_best
    theta_best = np.linalg.pinv(X_b.T @ X_b) @ X_b.T @ y_train

    # 手动预测函数
    def predict_manual(X):
        X = X.values  # 转换为 NumPy 数组
        X_b_test = np.c_[np.ones((X.shape[0], 1)), X]
        return X_b_test @ theta_best

    # 计算手动最小二乘法的预测值
    y_manual_pred = predict_manual(X_test)

    # 计算手动实现的 R^2 和 MSE
    r2_manual = r2_score(y_test, y_manual_pred)
    mse_manual = mean_squared_error(y_test, y_manual_pred)

    return r2_manual, mse_manual, theta_best, y_manual_pred

第六步： 将预测值的真实值的关系使用 matplotlib 绘制散点图进行 可视化

1
2
3
4
5
6
7
8
9
10
def draw_plot_map():
    # 可视化预测结果
    plt.scatter(y_test, y_pred, label="Sklearn Predict", alpha=0.5)
    plt.scatter(y_test, y_manual_pred, label="Manual Least Squares Predict", alpha=0.5, marker="x")
    plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--')
    plt.xlabel("True orbital period")
    plt.ylabel("Predicted orbital period")
    plt.title("Prediction vs True value (Log Transformed)")
    plt.legend()
    plt.show()

第七步： 输出最终的线性方程参数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def output():
    # 输出结果
    print("Sklearn 线性回归模型：")
    print(f"权重: {intercept_sklearn}")
    print(f"偏置: {coef_sklearn}")
    print(f"R²: {r2_sklearn}")
    print("log10(MSE):", log_mse_sklearn)
    print(f"Sklearn: y = {model.intercept_:.4f} + {model.coef_[0]:.4f} * pl_orbsmax + {model.coef_[1]:.4f} * st_mass")
    print("------------------------------------------------------")
    print("手动最小二乘法模型：")
    print(f"计算出的 theta_best: {theta_best.flatten()}")
    print(f"R²: {r2_manual}")
    print("log10(MSE):", log_mse_manual)
    print(f"Manual: y = {theta_best[0]:.4f} + {theta_best[1]:.4f} * pl_orbsmax + {theta_best[2]:.4f} * st_mass")

第八步： 对数据进行对数变换，然后重复第二到七步，获得模型效果，进行对比

在 天体问题 中，习惯的对数变换是以 10为底数 的变换，更符合天文物理学的习惯。与此同时，取对数可以更直观地对应开普勒定律。
这里需要时刻注意何时使用 对数后的数据 何时使用 原数据

具体使用代码来实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def pre():
    """训练前的数据处理"""
    
    #其余部分不变，略去

    # 进行 log10 对数变换
    X_log10 = np.log10(X)
    y_log10 = np.log10(y)

    # 拆分训练集和测试集
    X_train, X_test, y_train, y_test = train_test_split(X_log10, y_log10, test_size=0.2, random_state=42)

    return X_train, X_test, y_train, y_test

def sklearn(X_train, X_test, y_train, y_test):
    # 使用 sklearn 进行线性回归
    model = LinearRegression()
    model.fit(X_train, y_train)

    # 预测
    y_pred_log = model.predict(X_test)

    # 反变换回原始尺度
    y_pred = 10 ** y_pred_log

    # 计算 sklearn 线性回归的 R^2 和 MSE,注意在 log10 尺度计算 R^2 ，MSE 需要在原尺度计算
    r2_sklearn = r2_score(y_test, y_pred_log)
    mse_sklearn = mean_squared_error(10 ** y_test, y_pred)

    return r2_sklearn, mse_sklearn, model, y_pred

第九步： 解释模型的误差

各个系数的物理含义：
回归方程：
[
\log_{10} pl_orbper = 2.5611 + 1.4962 \log_{10} pl_orbsmax - 0.4700 \log_{10} st_mass
]
对比理论的开普勒第三定律：
[
pl_orbper = C \cdot pl_orbsmax^{3/2} \cdot st_mass^{-1/2}
]
取对数：
[
\log_{10} pl_orbper = \log_{10} C + 1.5 \log_{10} pl_orbsmax - 0.5 \log_{10} st_mass
]
其中，偏置项 代表：
[
\log_{10} C
]
所以，我们可以反推：
[
C = 10^{2.5611} \approx 363
]

开普勒定律的系数 C 取决于单位, 在以 AU、天和太阳质量 为单位的时候， 理论值为365.25
而由公式可得，另两个参数的理论值应该分别为 1.5 和 -0.5

最终的参数 实际值 和 理论值 对比:
$363 \approx 365.25 $
$1.4962 \approx 1.5$
$-0.4700 \approx -0.5$

尽管各个系数非常接近 理论值，但不完全一致，可能有几个原因：

  1. 数据误差
    • 测量数据可能有误差，导致拟合出的参数略有偏差
  2. 情况复杂
    • 理论上行星轨道只受到半径和质量的影响，但是在现实情况下，会受到其他天体（附近的行星）的引力扰动，这使得产生了噪声

如果希望修复这问题，我有以下两个思路：

  1. 增大数据量
    • 通过增大训练的数据量，可以一定程度上减少测量带来的误差影响
  2. 删除噪声过大的数据
    • 对于某些行星而言，其运动周期受到其他天体影响过于巨大，对于这样的天体再纳入训练只会起到反面作用。
    • 可以通过计算数据的 残差 ，然后删除掉残差超过设定的 阈值 的数据，即噪声过大的数据来实现更精准的模型

代码

不经过对数处理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

def pre():
    """训练前的数据处理"""
    # 加载数据
    df = pd.read_csv("D:/lianshidaiRecurit/03/PSCompPars.csv")

    # 处理缺失值
    df = df.dropna(subset=['pl_orbsmax', 'st_mass', 'pl_orbper'])

    # 提取相关特征和目标变量
    X = df[['pl_orbsmax', 'st_mass']]
    y = df['pl_orbper']

    # 拆分训练集和测试集
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

    return X_train, X_test, y_train, y_test

def sklearn(X_train, X_test, y_train, y_test):
    # 使用 sklearn 进行线性回归
    model = LinearRegression()
    model.fit(X_train, y_train)

    # 预测
    y_pred = model.predict(X_test)

    # 计算 sklearn 线性回归的 R^2 和 MSE
    r2_sklearn = r2_score(y_test, y_pred)
    mse_sklearn = mean_squared_error(y_test, y_pred)

    return r2_sklearn, mse_sklearn, model, y_pred

def manual(X_train, X_test, y_train, y_test):
    """手动实现最小二乘法计算参数"""
    # 偏置项
    X_b = np.c_[np.ones((len(X_train), 1)), X_train.values]
    # 伪逆法求解 theta_best
    theta_best = np.linalg.pinv(X_b.T @ X_b) @ X_b.T @ y_train

    # 手动预测函数
    def predict_manual(X):
        X = X.values  # 转换为 NumPy 数组
        X_b_test = np.c_[np.ones((X.shape[0], 1)), X]
        return X_b_test @ theta_best

    # 计算手动最小二乘法的预测值
    y_manual_pred = predict_manual(X_test)

    # 计算手动实现的 R^2 和 MSE
    r2_manual = r2_score(y_test, y_manual_pred)
    mse_manual = mean_squared_error(y_test, y_manual_pred)

    return r2_manual, mse_manual, theta_best, y_manual_pred

def output():
    # 输出结果
    print("Sklearn 线性回归模型：")
    print(f"权重: {intercept_sklearn}")
    print(f"偏置: {coef_sklearn}")
    print(f"R²: {r2_sklearn}")
    print("log10(MSE):", log_mse_sklearn)
    print(f"Sklearn: y = {model.intercept_:.4f} + {model.coef_[0]:.4f} * pl_orbsmax + {model.coef_[1]:.4f} * st_mass")
    print("------------------------------------------------------")
    print("手动最小二乘法模型：")
    print(f"计算出的 theta_best: {theta_best.flatten()}")
    print(f"R²: {r2_manual}")
    print("log10(MSE):", log_mse_manual)
    print(f"Manual: y = {theta_best[0]:.4f} + {theta_best[1]:.4f} * pl_orbsmax + {theta_best[2]:.4f} * st_mass")

def draw_plot_map():
    # 可视化预测结果
    plt.scatter(y_test, y_pred, label="Sklearn Predict", alpha=0.5)
    plt.scatter(y_test, y_manual_pred, label="Manual Least Squares Predict", alpha=0.5, marker="x")
    plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--')
    plt.xlabel("True orbital period")
    plt.ylabel("Predicted orbital period")
    plt.title("Prediction vs True value (Log Transformed)")
    plt.legend()
    plt.show()

if __name__=="__main__":
    X_train, X_test, y_train, y_test = pre()
    r2_sklearn, mse_sklearn, model, y_pred = sklearn(X_train, X_test, y_train, y_test)
    r2_manual, mse_manual, theta_best, y_manual_pred = manual(X_train, X_test, y_train, y_test)

    # 计算 MSE 时使用 log10 ，避免数值过大
    log_mse_sklearn = np.log10(mse_sklearn)
    log_mse_manual = np.log10(mse_manual)

    # 获取回归系数
    intercept_sklearn = model.intercept_
    coef_sklearn = model.coef_
    intercept_manual = theta_best[0]
    coef_manual = theta_best[1:]

    output()
    draw_plot_map()
经过对数处理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

def pre():
    """训练前的数据处理"""
    # 加载数据
    df = pd.read_csv("D:/lianshidaiRecurit/03/PSCompPars.csv")

    # 处理缺失值
    df = df.dropna(subset=['pl_orbsmax', 'st_mass', 'pl_orbper'])

    # 提取相关特征和目标变量
    X = df[['pl_orbsmax', 'st_mass']]
    y = df['pl_orbper']

    # 进行 log10 对数变换
    X_log10 = np.log10(X)
    y_log10 = np.log10(y)

    # 拆分训练集和测试集
    X_train, X_test, y_train, y_test = train_test_split(X_log10, y_log10, test_size=0.2, random_state=42)

    return X_train, X_test, y_train, y_test

def sklearn(X_train, X_test, y_train, y_test):
    # 使用 sklearn 进行线性回归
    model = LinearRegression()
    model.fit(X_train, y_train)

    # 预测
    y_pred_log = model.predict(X_test)

    # 反变换回原始尺度
    y_pred = 10 ** y_pred_log

    # 计算 sklearn 线性回归的 R^2 和 MSE,注意在 log10 尺度计算 R^2 ，MSE 需要在原尺度计算
    r2_sklearn = r2_score(y_test, y_pred_log)
    mse_sklearn = mean_squared_error(10 ** y_test, y_pred)

    return r2_sklearn, mse_sklearn, model, y_pred

def output():
    # 输出结果
    print("Sklearn 线性回归模型：")
    print(f"权重: {intercept_sklearn}")
    print(f"偏置: {coef_sklearn}")
    print(f"R²: {r2_sklearn}")
    print("log10(MSE):", log_mse_sklearn)
    print(f"Sklearn: log10(y) = {model.intercept_:.4f} + {model.coef_[0]:.4f} * log10(pl_orbsmax) + {model.coef_[1]:.4f} * log10(st_mass)")

def draw_plot_map():
    # 可视化预测结果
    plt.scatter(10 ** y_test, y_pred, label="Sklearn Predict", alpha=0.5)
    plt.plot([(10 ** y_test).min(), (10 ** y_test).max()], [(10 ** y_test).min(), (10 ** y_test).max()], 'r--')
    plt.xlabel("True orbital period")
    plt.ylabel("Predicted orbital period")
    plt.title("Prediction vs True value (Log Transformed)")
    plt.legend()
    plt.show()


if __name__ == "__main__" :
    X_train, X_test, y_train, y_test = pre()
    r2_sklearn, mse_sklearn, model, y_pred = sklearn(X_train, X_test, y_train, y_test)

    log_mse_sklearn = np.log10(mse_sklearn)

    # 获取回归系数
    intercept_sklearn = model.intercept_
    coef_sklearn = model.coef_

    output()
    draw_plot_map()

结果

对数变化前：

alt text

对数变化后：

alt text

project
|