预测系外行星轨道周期

project

任务

  • 使用 NASA系外行星数据库 中的数据
  • 选取轨道半长轴（pl_orbsmax）和母恒星质量（st_mass）作为输入特征
  • 目标变量为轨道周期（pl_orbper）

思路

导入必要的库

1
2
3
4
5
6
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

第一步： 访问 NASA 系外行星数据库，获取行星数据保存在 csv 文件中
第二步： 提取 csv 文件中所需要的数据，保留’pl_orbsmax’, ‘st_mass’和’pl_orbper’数据，与此同时注意到某些数据是缺失的，故而使用 df.dropna(subset=['pl_orbsmax', 'st_mass', 'pl_orbper']) 用来删除含有缺失值的数据组，保证后续计算正确

1
2
3
4
5
6
7
8
9
# 加载数据
df = pd.read_csv("D:/lianshidaiRecurit/03/PSCompPars_2025.02.09_07.27.02.csv")

# 处理缺失值
df = df.dropna(subset=['pl_orbsmax', 'st_mass', 'pl_orbper'])

# 选择相关特征和目标变量
X = df[['pl_orbsmax', 'st_mass']]
y = df['pl_orbper']

第三步： 使用提取到的数据来训练模型

首先需要将数据使用 train_test_split 来拆分成 8：2 的训练集和测试集，使用训练集来进行线性回归拟合

1
2
3
4
5
6
7
8
9
# 拆分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 使用 sklearn 进行线性回归
model = LinearRegression()
model.fit(X_train, y_train)

# 预测
y_pred = model.predict(X_test)

第四步： 使用 MSE、R检测法 来评估模型的预测性能

1
2
3
4
5
6
# 预测
y_pred = model.predict(X_test)

# 计算 sklearn 线性回归的 R^2 和 MSE
r2_sklearn = r2_score(y_test, y_pred)
mse_sklearn = mean_squared_error(y_test, y_pred)

第五步： 手动使用最小二乘法来完成线性回归的任务，这里具体的计算方法使用了 伪逆矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def manual(X_train, X_test, y_train, y_test):
    """手动实现最小二乘法计算参数"""
    # 偏置项
    X_b = np.c_[np.ones((len(X_train), 1)), X_train.values]
    # 伪逆法求解 theta_best
    theta_best = np.linalg.pinv(X_b.T @ X_b) @ X_b.T @ y_train

    # 手动预测函数
    def predict_manual(X):
        X = X.values  # 转换为 NumPy 数组
        X_b_test = np.c_[np.ones((X.shape[0], 1)), X]
        return X_b_test @ theta_best

    # 计算手动最小二乘法的预测值
    y_manual_pred = predict_manual(X_test)

    # 计算手动实现的 R^2 和 MSE
    r2_manual = r2_score(y_test, y_manual_pred)
    mse_manual = mean_squared_error(y_test, y_manual_pred)

    return r2_manual, mse_manual, theta_best, y_manual_pred

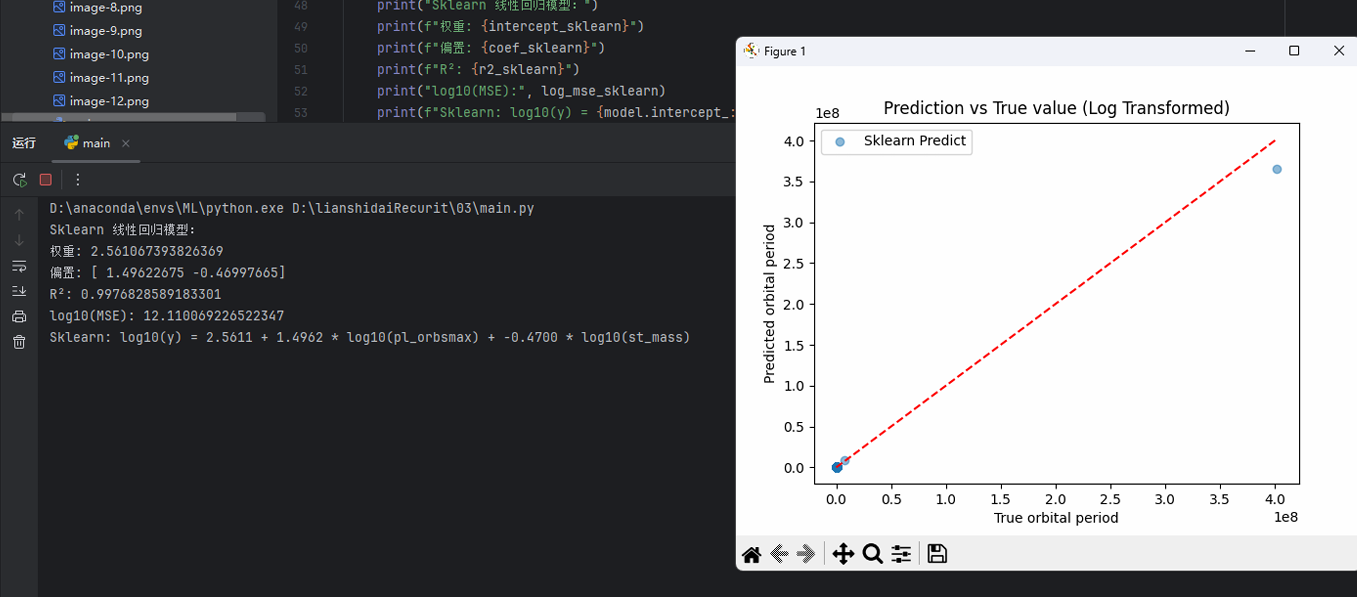
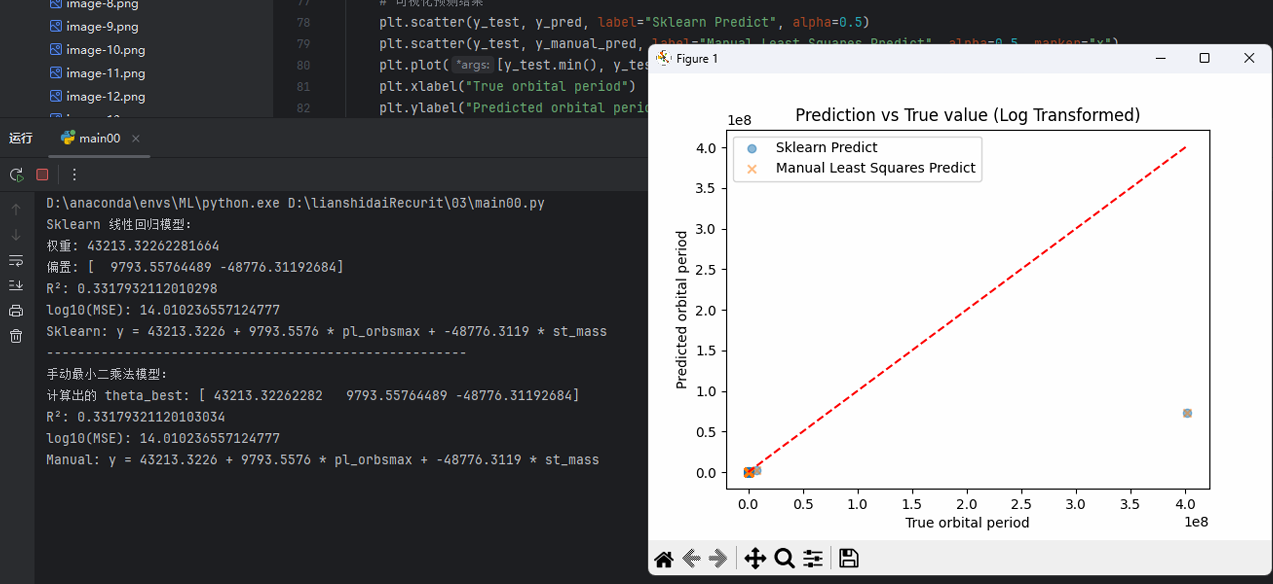
第六步： 将预测值的真实值的关系使用 matplotlib 绘制散点图进行 可视化

1
2
3
4
5
6
7
8
9
10
def draw_plot_map():
    # 可视化预测结果
    plt.scatter(y_test, y_pred, label="Sklearn Predict", alpha=0.5)
    plt.scatter(y_test, y_manual_pred, label="Manual Least Squares Predict", alpha=0.5, marker="x")
    plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--')
    plt.xlabel("True orbital period")
    plt.ylabel("Predicted orbital period")
    plt.title("Prediction vs True value (Log Transformed)")
    plt.legend()
    plt.show()

第七步： 输出最终的线性方程参数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def output():
    # 输出结果
    print("Sklearn 线性回归模型：")
    print(f"权重: {intercept_sklearn}")
    print(f"偏置: {coef_sklearn}")
    print(f"R²: {r2_sklearn}")
    print("log10(MSE):", log_mse_sklearn)
    print(f"Sklearn: y = {model.intercept_:.4f} + {model.coef_[0]:.4f} * pl_orbsmax + {model.coef_[1]:.4f} * st_mass")
    print("------------------------------------------------------")
    print("手动最小二乘法模型：")
    print(f"计算出的 theta_best: {theta_best.flatten()}")
    print(f"R²: {r2_manual}")
    print("log10(MSE):", log_mse_manual)
    print(f"Manual: y = {theta_best[0]:.4f} + {theta_best[1]:.4f} * pl_orbsmax + {theta_best[2]:.4f} * st_mass")

第八步： 对数据进行对数变换，然后重复第二到七步，获得模型效果，进行对比

在 天体问题 中，习惯的对数变换是以 10为底数 的变换，更符合天文物理学的习惯。与此同时，取对数可以更直观地对应开普勒定律。
这里需要时刻注意何时使用 对数后的数据 何时使用 原数据

具体使用代码来实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def pre():
    """训练前的数据处理"""
    
    #其余部分不变，略去

    # 进行 log10 对数变换
    X_log10 = np.log10(X)
    y_log10 = np.log10(y)

    # 拆分训练集和测试集
    X_train, X_test, y_train, y_test = train_test_split(X_log10, y_log10, test_size=0.2, random_state=42)

    return X_train, X_test, y_train, y_test

def sklearn(X_train, X_test, y_train, y_test):
    # 使用 sklearn 进行线性回归
    model = LinearRegression()
    model.fit(X_train, y_train)

    # 预测
    y_pred_log = model.predict(X_test)

    # 反变换回原始尺度
    y_pred = 10 ** y_pred_log

    # 计算 sklearn 线性回归的 R^2 和 MSE,注意在 log10 尺度计算 R^2 ，MSE 需要在原尺度计算
    r2_sklearn = r2_score(y_test, y_pred_log)
    mse_sklearn = mean_squared_error(10 ** y_test, y_pred)

    return r2_sklearn, mse_sklearn, model, y_pred

第九步： 解释模型的误差

各个系数的物理含义：
回归方程：
[
\log_{10} pl_orbper = 2.5611 + 1.4962 \log_{10} pl_orbsmax - 0.4700 \log_{10} st_mass
]
对比理论的开普勒第三定律：
[
pl_orbper = C \cdot pl_orbsmax^{3/2} \cdot st_mass^{-1/2}
]
取对数：
[
\log_{10} pl_orbper = \log_{10} C + 1.5 \log_{10} pl_orbsmax - 0.5 \log_{10} st_mass
]
其中，偏置项 代表：
[
\log_{10} C
]
所以，我们可以反推：
[
C = 10^{2.5611} \approx 363
]

开普勒定律的系数 C 取决于单位, 在以 AU、天和太阳质量 为单位的时候， 理论值为365.25
而由公式可得，另两个参数的理论值应该分别为 1.5 和 -0.5

最终的参数 实际值 和 理论值 对比:
$363 \approx 365.25 $
$1.4962 \approx 1.5$
$-0.4700 \approx -0.5$

尽管各个系数非常接近 理论值，但不完全一致，可能有几个原因：

  1. 数据误差
    • 测量数据可能有误差，导致拟合出的参数略有偏差
  2. 情况复杂
    • 理论上行星轨道只受到半径和质量的影响，但是在现实情况下，会受到其他天体（附近的行星）的引力扰动，这使得产生了噪声

如果希望修复这问题，我有以下两个思路：

  1. 增大数据量
    • 通过增大训练的数据量，可以一定程度上减少测量带来的误差影响
  2. 删除噪声过大的数据
    • 对于某些行星而言，其运动周期受到其他天体影响过于巨大，对于这样的天体再纳入训练只会起到反面作用。
    • 可以通过计算数据的 残差 ，然后删除掉残差超过设定的 阈值 的数据，即噪声过大的数据来实现更精准的模型

代码

不经过对数处理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

def pre():
    """训练前的数据处理"""
    # 加载数据
    df = pd.read_csv("D:/lianshidaiRecurit/03/PSCompPars.csv")

    # 处理缺失值
    df = df.dropna(subset=['pl_orbsmax', 'st_mass', 'pl_orbper'])

    # 提取相关特征和目标变量
    X = df[['pl_orbsmax', 'st_mass']]
    y = df['pl_orbper']

    # 拆分训练集和测试集
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

    return X_train, X_test, y_train, y_test

def sklearn(X_train, X_test, y_train, y_test):
    # 使用 sklearn 进行线性回归
    model = LinearRegression()
    model.fit(X_train, y_train)

    # 预测
    y_pred = model.predict(X_test)

    # 计算 sklearn 线性回归的 R^2 和 MSE
    r2_sklearn = r2_score(y_test, y_pred)
    mse_sklearn = mean_squared_error(y_test, y_pred)

    return r2_sklearn, mse_sklearn, model, y_pred

def manual(X_train, X_test, y_train, y_test):
    """手动实现最小二乘法计算参数"""
    # 偏置项
    X_b = np.c_[np.ones((len(X_train), 1)), X_train.values]
    # 伪逆法求解 theta_best
    theta_best = np.linalg.pinv(X_b.T @ X_b) @ X_b.T @ y_train

    # 手动预测函数
    def predict_manual(X):
        X = X.values  # 转换为 NumPy 数组
        X_b_test = np.c_[np.ones((X.shape[0], 1)), X]
        return X_b_test @ theta_best

    # 计算手动最小二乘法的预测值
    y_manual_pred = predict_manual(X_test)

    # 计算手动实现的 R^2 和 MSE
    r2_manual = r2_score(y_test, y_manual_pred)
    mse_manual = mean_squared_error(y_test, y_manual_pred)

    return r2_manual, mse_manual, theta_best, y_manual_pred

def output():
    # 输出结果
    print("Sklearn 线性回归模型：")
    print(f"权重: {intercept_sklearn}")
    print(f"偏置: {coef_sklearn}")
    print(f"R²: {r2_sklearn}")
    print("log10(MSE):", log_mse_sklearn)
    print(f"Sklearn: y = {model.intercept_:.4f} + {model.coef_[0]:.4f} * pl_orbsmax + {model.coef_[1]:.4f} * st_mass")
    print("------------------------------------------------------")
    print("手动最小二乘法模型：")
    print(f"计算出的 theta_best: {theta_best.flatten()}")
    print(f"R²: {r2_manual}")
    print("log10(MSE):", log_mse_manual)
    print(f"Manual: y = {theta_best[0]:.4f} + {theta_best[1]:.4f} * pl_orbsmax + {theta_best[2]:.4f} * st_mass")

def draw_plot_map():
    # 可视化预测结果
    plt.scatter(y_test, y_pred, label="Sklearn Predict", alpha=0.5)
    plt.scatter(y_test, y_manual_pred, label="Manual Least Squares Predict", alpha=0.5, marker="x")
    plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--')
    plt.xlabel("True orbital period")
    plt.ylabel("Predicted orbital period")
    plt.title("Prediction vs True value (Log Transformed)")
    plt.legend()
    plt.show()

if __name__=="__main__":
    X_train, X_test, y_train, y_test = pre()
    r2_sklearn, mse_sklearn, model, y_pred = sklearn(X_train, X_test, y_train, y_test)
    r2_manual, mse_manual, theta_best, y_manual_pred = manual(X_train, X_test, y_train, y_test)

    # 计算 MSE 时使用 log10 ，避免数值过大
    log_mse_sklearn = np.log10(mse_sklearn)
    log_mse_manual = np.log10(mse_manual)

    # 获取回归系数
    intercept_sklearn = model.intercept_
    coef_sklearn = model.coef_
    intercept_manual = theta_best[0]
    coef_manual = theta_best[1:]

    output()
    draw_plot_map()
经过对数处理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

def pre():
    """训练前的数据处理"""
    # 加载数据
    df = pd.read_csv("D:/lianshidaiRecurit/03/PSCompPars.csv")

    # 处理缺失值
    df = df.dropna(subset=['pl_orbsmax', 'st_mass', 'pl_orbper'])

    # 提取相关特征和目标变量
    X = df[['pl_orbsmax', 'st_mass']]
    y = df['pl_orbper']

    # 进行 log10 对数变换
    X_log10 = np.log10(X)
    y_log10 = np.log10(y)

    # 拆分训练集和测试集
    X_train, X_test, y_train, y_test = train_test_split(X_log10, y_log10, test_size=0.2, random_state=42)

    return X_train, X_test, y_train, y_test

def sklearn(X_train, X_test, y_train, y_test):
    # 使用 sklearn 进行线性回归
    model = LinearRegression()
    model.fit(X_train, y_train)

    # 预测
    y_pred_log = model.predict(X_test)

    # 反变换回原始尺度
    y_pred = 10 ** y_pred_log

    # 计算 sklearn 线性回归的 R^2 和 MSE,注意在 log10 尺度计算 R^2 ，MSE 需要在原尺度计算
    r2_sklearn = r2_score(y_test, y_pred_log)
    mse_sklearn = mean_squared_error(10 ** y_test, y_pred)

    return r2_sklearn, mse_sklearn, model, y_pred

def output():
    # 输出结果
    print("Sklearn 线性回归模型：")
    print(f"权重: {intercept_sklearn}")
    print(f"偏置: {coef_sklearn}")
    print(f"R²: {r2_sklearn}")
    print("log10(MSE):", log_mse_sklearn)
    print(f"Sklearn: log10(y) = {model.intercept_:.4f} + {model.coef_[0]:.4f} * log10(pl_orbsmax) + {model.coef_[1]:.4f} * log10(st_mass)")

def draw_plot_map():
    # 可视化预测结果
    plt.scatter(10 ** y_test, y_pred, label="Sklearn Predict", alpha=0.5)
    plt.plot([(10 ** y_test).min(), (10 ** y_test).max()], [(10 ** y_test).min(), (10 ** y_test).max()], 'r--')
    plt.xlabel("True orbital period")
    plt.ylabel("Predicted orbital period")
    plt.title("Prediction vs True value (Log Transformed)")
    plt.legend()
    plt.show()


if __name__ == "__main__" :
    X_train, X_test, y_train, y_test = pre()
    r2_sklearn, mse_sklearn, model, y_pred = sklearn(X_train, X_test, y_train, y_test)

    log_mse_sklearn = np.log10(mse_sklearn)

    # 获取回归系数
    intercept_sklearn = model.intercept_
    coef_sklearn = model.coef_

    output()
    draw_plot_map()

结果

对数变化前：

alt text

对数变化后：

alt text

Title:预测系外行星轨道周期

Author:

Created:2025-02-27, 22:25:05

Updated:2025-03-24, 15:37:50

Full URL:http://example.com/2025/02/27/%E9%A2%84%E6%B5%8B%E7%B3%BB%E5%A4%96%E8%A1%8C%E6%98%9F%E8%BD%A8%E9%81%93%E5%91%A8%E6%9C%9F/

License: "CC BY-NC-SA 4.0" Keep Link & Author if Distribute.

Contents
  1. 1. 任务
  2. 2. 思路
  3. 3. 代码
    1. 3.0.0.1. 不经过对数处理
    2. 3.0.0.2. 经过对数处理
  • 4. 结果
    • |